第四章 绘制灰色方阵

本章为游戏添加灰色方格背景。通过绘制灰色方阵，来学习编程语言中非常重要的语句——循环语句。

第一节 方阵中的数学问题

如图4-1所示，我们将画布宽度设为300像素，高度为400像素，每个方块的宽和高都是24像素，且方块之间有1个像素的空白间隔，这样整个画布就被划分为16行，每行有12个方块，整个屏幕上共有16×12=192个方块。让我们先来确定第一行12个方块的位置。在上一章中，我们已经知道了如何确定画笔的起点及终点坐标，这里将它们列在表格4-1中。

表4-1 灰格方阵中第一行12列个灰色方格的起点及终点坐标

在上面表格中，无论是起点，还是终点，y的坐标值都等于12，但x的坐标值呈现出有规律的变化，即，相邻的两个块之间x坐标的差值为25，并且与列数有某种相关性。具体来说，如果用J来表示列数，则第J列起点及终点的x坐标值分别可以表示为： 起点x坐标 = (J-1)×25 终点x坐标 = J×25-1 以第7列为例，即当J=7时，起点的x坐标=(7-1)×25=150，终点的x坐标=7×25-1=174。

对于学习过代数知识的初中以上的学生来说，这是一个非常简单的公式提取过程。在几乎所有的游戏开发中，都会遇到提取公式的问题，因此提取公式是一个游戏开发者最基本的能力。不过，小学生们也不必担心，你可以观察一组数字的变化规律，然后尝试把你看到的规律用公式表示出来，再用实际的数据加以验证，这正是培养自己抽象思维能力的好机会。

下面再来确定第2、3乃至第16行中方块的位置，如表4-2所示。

表4-2 第1、2、3及16行方块的位置（画线的起点及终点坐标）

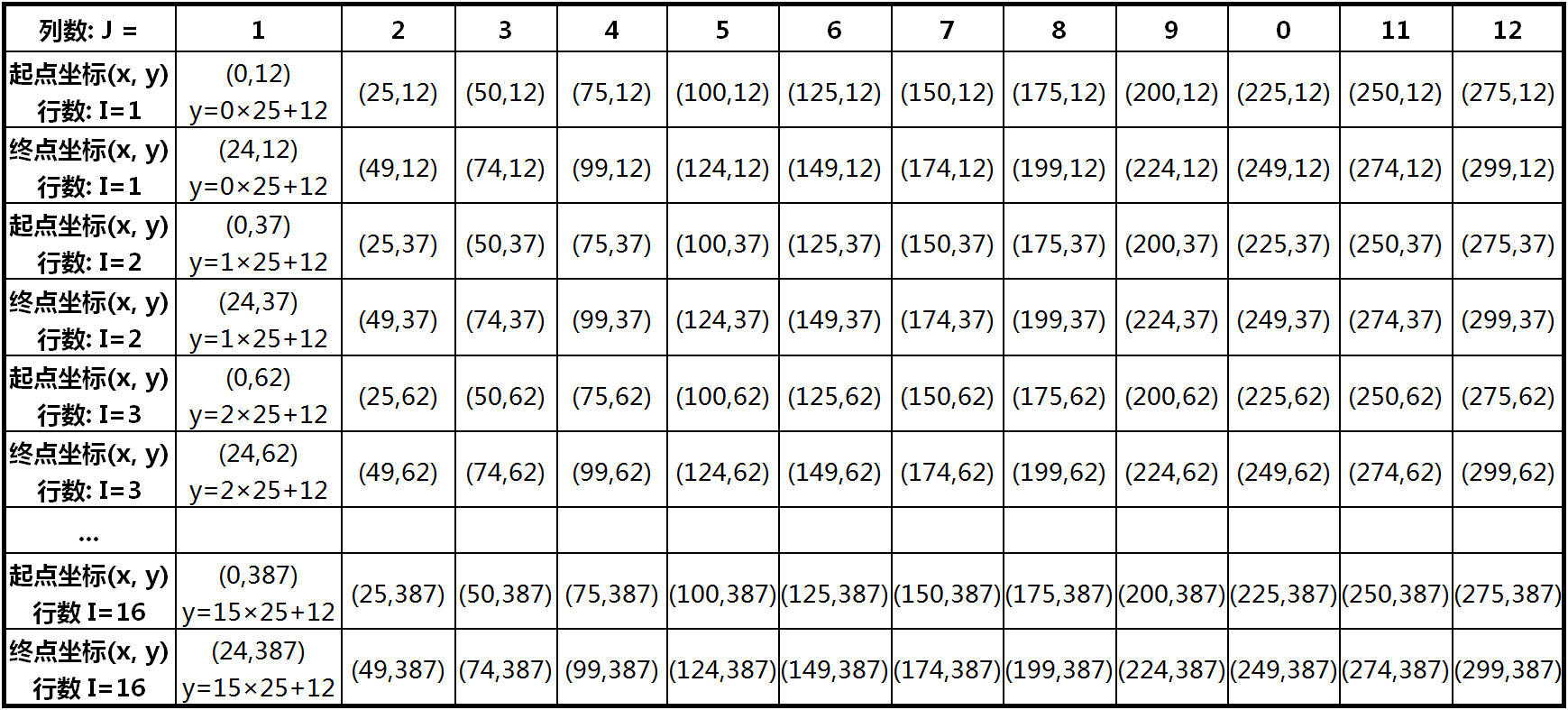
上表给出了第1、2、3行及第16行方块的位置，也就是绘制方块时起点及终点的坐标。这里每一行x坐标的变化规律与上面讨论过的第一行完全相同，而y坐标的变化规律同样体现为两个方面：一是相邻两行之间y坐标的差值为25，二是y坐标值与行数有着某种相关性。具体来说，如果用I来表示行数，则第I行的y坐标可以表示为

y = (I-1)×25+12

以第16行为例，当I=16时，方块起点及终点的y坐标=(16-1)×25+12 = 387。

到目前为止，我们可以用公式表示出任意行 i 、任意列 j 处的方块的起点及终点坐标值，其公式为：

起点 x = (j-1)×25，起点 y = (i-1)×25+12
终点 x = j×25-1，   终点 y = (i-1)×25+12

有了上面的公式，我们可以开始绘制方阵了。

第二节 绘制方阵

在绘制方阵之前，我们来设置Screen1的水平对齐属性，由默认的“居左”改为“居中”，以便让画布显示在屏幕正中，与屏幕的左右两侧保持等距。

我们要绘制192个方块（12×16），先让我们绘制第一行的四个方块，如图4-2所示。

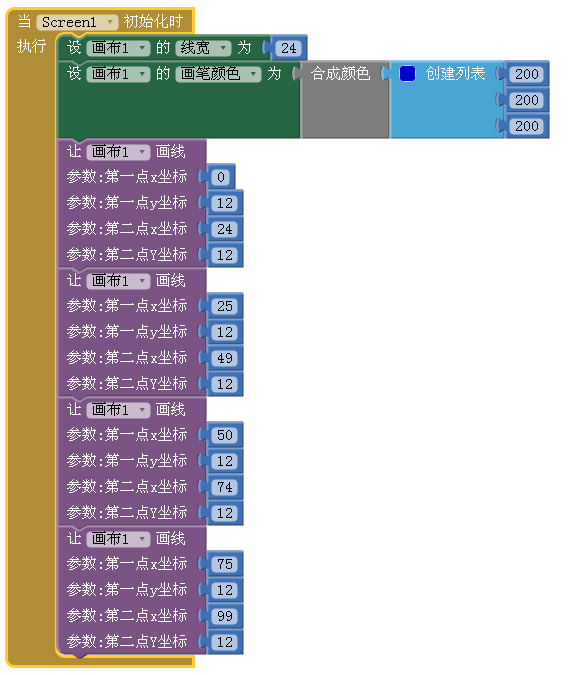
在图4-2A的代码中，我们首先设置了画布的线宽（24像素），再将画笔的颜色设置为浅灰色，即RGB的值为(200,200,200)，然后分别绘制了四个方块，绘制的结果在测试手机上的效果如图4-2B所示。

显然，我们不可能调用192次画布的画线功能，App Inventor提供了重复执行类似命令的循环语句，它属于内置的控制类代码块（位居第二）。这是一个非常重要的语句块，在几乎所有程序中，都少不了循环语句的使用。下面我们用它来绘制第一行的方块。如图4-3所示。

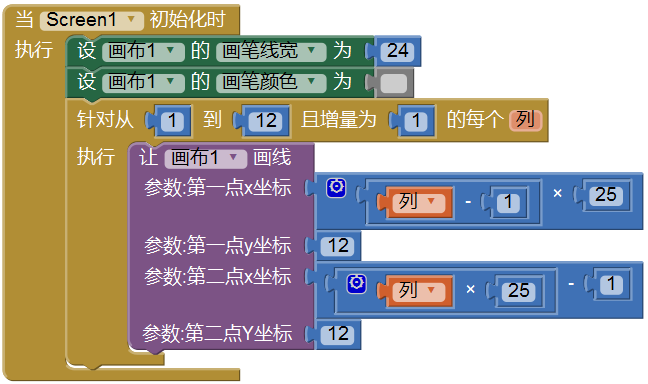
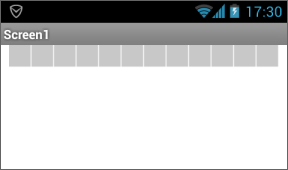
在上述代码块中，“针对从1到12且增量为1的每个列，执行...”块就是前面提到的循环语句，它包含了“让画布1画线”块。

所谓“循环”就是反复执行，块中的“列”被称为循环变量，在这里，循环变量的初始值为1，最大值为12，增量为1。整个循环语句的执行顺序是：当第一次循环开始执行时，列=1，当第一次循环执行结束时，为循环变量+1，此时，列=2，并准备开始执行第二次循环；每当准备开始一次新的循环时，要将循环变量的当前值（列）与最大值（12）进行比较，如果当前值小于或等于最大值，则执行循环体内的语句，如果当前值大于最大值，则退出循环，并执行循环体之后的语句。因此在上述代码中，共进行了12次循环，在第12次循环结束时，循环变量值增加到13，不再满足循环执行的条件，因此程序将退出循环。

在“让画布1画线”语句中，我们用循环变量“列”来代替表4-1公式中的J，实现了每隔25个像素绘制一个方块的目标。

接下来我们还有更高的目标，就是在画布上绘制16个上面的方块行。想想看，怎么来做。

其实每一行的绘制方法都是类似的，其中每一行中12个方块的x坐标值都是一组相同的数列（0,25,50,...,275），不同的是y的坐标值，第一行12，第二行25+12，第三行25×2+12...等等，那么我们能不能再写一个循环语句，将上面的画一行块的语句包含起来呢？回答是肯定的。我们来看图4-4中的代码。

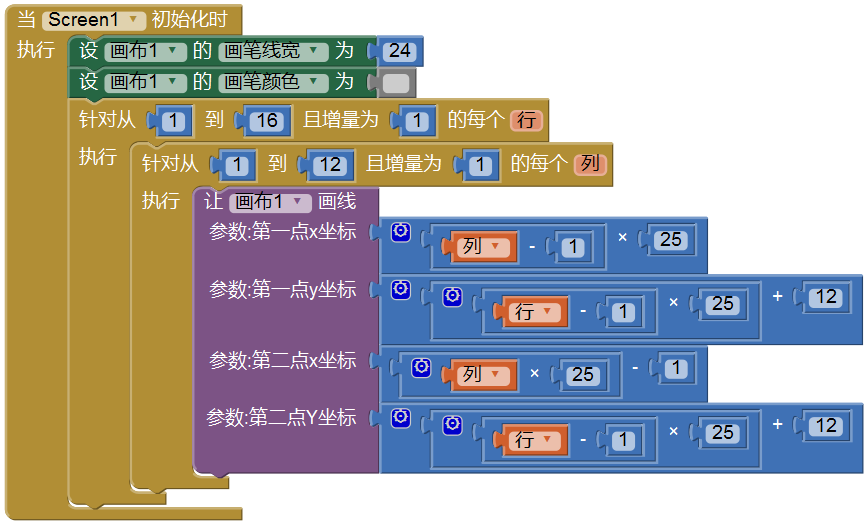
利用画布的画线功能及块语言的双重循环语句，我们已经成功地绘制了一个灰格方阵，这些灰色的格子是画布的背景，也是接下来我们开发的游戏的背景。

第三节 逐步了解开发工具

本节介绍编程语言中非常重要的一个概念：变量，并对循环语句做进一步的解释。

一、什么是变量

顾名思义，变量就是变化的量，它表明某项数据具有可变性。但在编程语言中，仅用“变化”还不足以说明变量的特征，它还包含了另外两重含义，一是赋予数据一个贴切的名字；二是为数据提供一个临时的寄存处。

在编程语言中，核心的任务是处理数据，对于那些只使用一次的数据，由于数据本身无需在各段程序中共享，因此也就无需将它们临时寄存，并赋予它们名字；但当一项数据要被多次使用时，就需要给它一个名字，并将它寄存在某处，以便需要的时候，其它程序可以随时访问它。

计算机中的数据保存方式有两种，一种是永久保存，如保存在硬盘上的文件，另一种是临时保存，即，保存在计算机的内存中。保存在内存中的数据，会因计算机的关闭而消失。在程序运行过程中，它所处理的大部分数据，都存放在内存中。变量的值被保存在某个“房间”（一小块内存空间）里，同时给这个“房间”取一个有意义的名字，程序就用这个名字来提取或修改变量的值。虽然内存中的每个“房间”都具有一个独一无二的地址，但高级的编程语言从来不使用这些地址，就像我们每个人虽然都有一个独一无二的身份证号码，但我们却从来不用它来与人交流，我们用自己的名字与人交流。

以上的叙述有些抽象，你也许会感到迷惑，究竟什么是变量呢？其实非常简单，在我们刚刚编写的代码中，就使用了两个变量：“行”和“列”。

在图4-5，橙色区域中的文字就是变量的名字，它们的值分别代表了方块 所在的行和列，在程序的运行过程中，它们的值不断地被改变（+1），并被多次读取，用来计算在“画布1”上画线时的起点和终点位置。

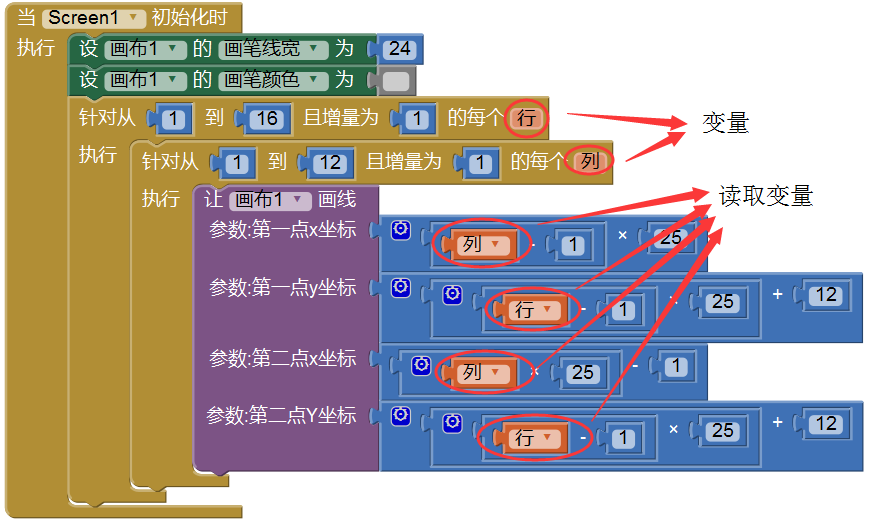
在后续的章节中，我们还会用到更多的变量，变量的值有简单与复杂之分，变量的适用范围有全局与局部之分，此外，变量的身份有独立于附属之分，下面将简单地介绍一下变量的分类。

二、变量的分类

1) 简单变量与复杂变量

在上一章中我们了解到，在App Inventor中有五种类型的数据：数字、文字、逻辑、颜色及列表，其中前四种为简单数据类型，而列表则为复杂数据类型，变量的分类也是如此。当变量中保存的数据是简单类型时，该变量即为简单变量；当变量中保存的数据为列表时，则称其为复杂变量。

2) 全局变量与局部变量

全局变量与局部变量的差别在于其可用（或可见）范围。所谓全局变量，指的是在整个程序的任何一处都可以调用的变量，而局部变量只能在某段特定的程序中有效。

3) 独立变量与附属变量

全局变量和局部变量都是独立变量，在使用之前需要进行显式声明，App Inventor分别提供了三种代码块，用来显式地声明全局变量和局部变量，如图4-6所示。而附属变量是某些代码块自带的变量，如上一节中我们用到的“行”、“列”，它们附属于循环语句，使用前无需显式声明，由App Inventor自动声明，并且只在循环语句内有效。               

三、变量的声明

独立变量——全局变量及局部变量，在使用前必须进行显式地声明，声明的目的是为变量取名，同时为变量设定一个初始值，如图4-7所示。而附属变量在使用前无需显式声明，它的声明由App Inventor自动完成。

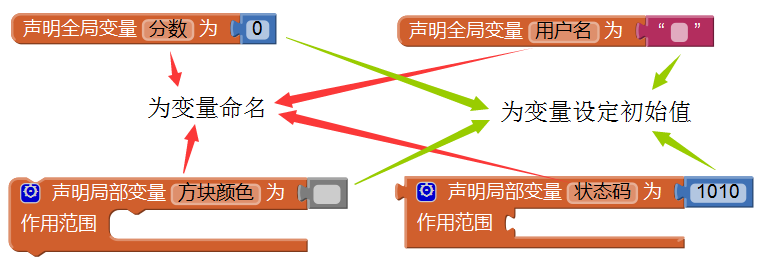
四、变量的读写操作

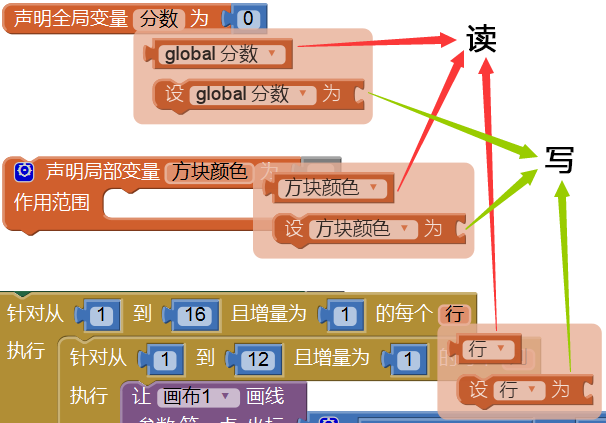
对变量的操作只有两种：一个是“读”，一个是“写”。“读”可以理解为获取变量的当前值，“写”则是改写（修改）变量的当前值。在App Inventor中，从变量的声明语句中，派生出变量的读写语句。如图4-8所示，当鼠标悬停在变量名上时，变量名的下方会自动弹出两个代码块：“global 变量名”及“设 global 变量名为”，其中前者为“读”操作，后者为“写”操作。

五、循环语句

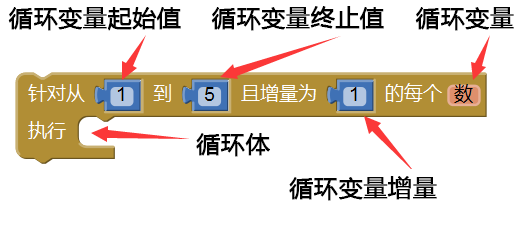
循环语句是所有编程语言中都具备的一个语句，用于重复执行一段程序，这段被重复执行的程序叫做循环体。循环语句中包含五个基本要素：

1. 循环变量
2. 循环变量增量
3. 循环变量起始值
4. 循环变量终止值
5. 循环体

循环语句的执行过程包括四个步骤：

1. 读取循环变量初始值
2. 执行循环体
3. 为循环变量值加上增量值
4. 判断循环变量值是否超出了循环变量的终止值
   • 如果不超出，则开始执行下一轮循环
   • 如果超出，则终止循环

其中第一步仅执行一次，而2~4步会反复执行直到循环结束。这里举一个简单的例子，帮助理解循环语句的执行过程。

有这样一道题，求从1到100之间所有自然数的和。求和的循环语句如图4-10所示。

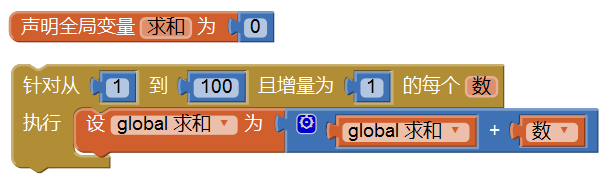
下面对问题做一下改动，求从1到100之间所有偶数的和。

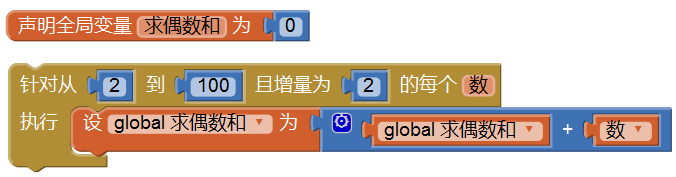
注意到有几点变化：

1. 循环变量的初始值从1变为2；
2. 循环变量增量从1变为2； 我们还可以求从1到100的所有奇数的和，等等。有兴趣的同学可以自己在App Inventor中做一个小程序，将计算结果显示出来。

小结

• 坐标公式的提取：用代数的方法表示画布上192个方块的绘制坐标；
• 循环语句：让类似的操作指令循环执行，通过循环变量的改变，来体现指令的差别；
• 变量：对于那些需要在多处或多次使用的可变数据，将它们寄存在内存中，并取名字以利于操作。