第十章 消除填满行的方块

在开始新的一章之前，我们先来回顾一下之前已经完成的程序，如图10-1所示：为这些代码分类，是为了强调要分别处理不同类型的操作，保持代码功能的单纯性，避免重复操作，也便于对代码中错误的查找。

在这一章中，我们要在组块触底或触块之后加入新的判断：所有已经触底的组块是否已经填满了一行或多行。如果填满，则消除那些已经填满的行，并让上面未填满的行落下来。

第一节 判断是否有填满的行

当一个组块触底后，它可能刚好填补了一个空缺，使得画布上有了填满的行，如图10-2中的左侧的那个黄色区域。当这个组块触底后，画布上最下方的四个行被填满。我们的程序需要首先确定触底组块所覆盖的区域，准确来说，是它占据的行；其次对这些行进行判断，如果这些行中不存在灰色方块，则意味着被填满。我们希望定义一个新的过程“ 求填满的行”，这个过程具有返回值，返回值是一个列表，列表项为被填满的行的行号。

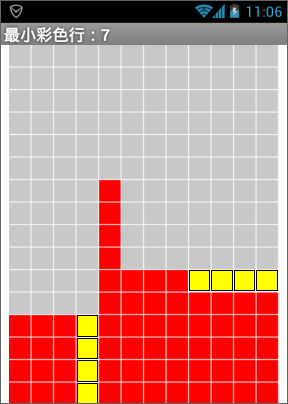
让我们先脱离开编程环境，单靠头脑的思考来构造出这个过程。从哪里开始呢？我们应该清醒地意识到，游戏中所有重要的数据，或者说任意时刻游戏的状态，都保存在全局变量中，而画布上那些方块的颜色码则保存在全局变量色块列表之中，因此我们的思路将从这里开始。色块列表中包含了192个列表项，每一项的值为一个颜色的代码，通过遍历某些行的列表项，来检测其颜色码，从而得知某一行是否已被填满。具体来说，当某一行中没有灰色方块时，即，某一行中的所有列表项的值都≠0时，则该行被填满。

有了上面的分析，下面我们进入App Inventor的编程视图，来实现这些思考。最终的代码如图10-3所示。在图10-4中，我们提供了该程序的流程图，可以更清楚地描述程序的执行过程。

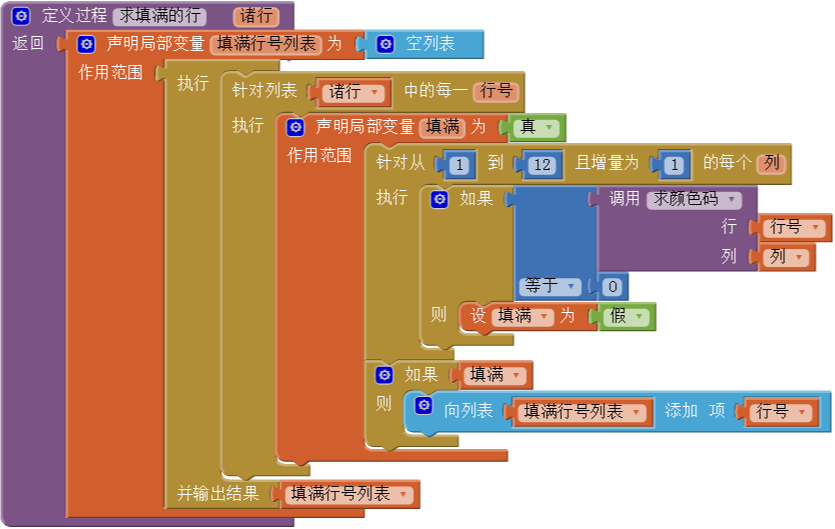
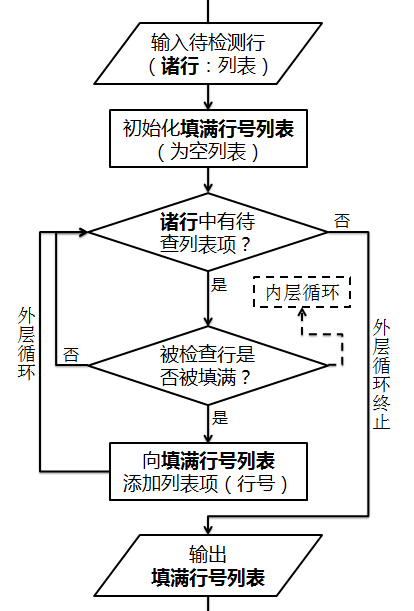
过程求填满的行既有输入（参数诸行，是一个待检测行的行号列表），也有输出（填满行的行号列表）。程序首先声明一个局部变量“填满行号列表”，并设其初始值为空列表。然后我们使用了一个执行...返回结果的语句块，这个语句等同于一个有返回值的过程，但因为所要执行的语句在整个程序中只使用一次，也就是说，这部分代码不具备复用的价值，因此不必创建一个独立的过程。在执行...返回结果语句中，我们使用了双重循环语句。你可能已经注意到，外层循环不再像以往一样“针对从1到16且增量为1的每一行”，而是“针对列表诸行中的每一行号”。这是另一种类型的循环语句——专门用于列表的循环语句，它所做的是对所有列表项进行遍历，直到遍历完成，这里是对待检测的诸行列表进行遍历。在外层循环与内层循环之间声明了一个局部变量填满，每当开始检测新的一行时，先假设其值为真（已经填满），当遍历过程中遇到灰色方块时（颜色码=0），设其值为假；紧接着，如果填满值为真，则向填满行号列表中添加一个列表项——被填满行的行号；当诸行列表中的所有列表项都被检测过之后，外层循环终止，并输出填满行号列表，程序结束。

从效果上讲，外层循环也可以使用“针对从1到16且增量为1”的循环语句，这时可以省去过程的输入项诸行，这样输出的结果是一样的，但是程序在运行时的计算量至少要四倍于列表遍历循环，而且多余的计算都是无效的计算（想想为什么？）。

有了这个过程，接下来要考虑两件问题：①在哪里调用这个过程；②如何利用这个过程的结果，来消除这些被填满的行。

先来解决第一个问题，在哪里调用这个过程。我们的思考沿着以下线索进行：

• 首先，组块的任何行为都发生在计时程序中；
• 其次，在计时程序中，有四处组块停止下落判断：1、2号组块的触底、触块判断；
• 当停止下落判断为真时，首先调用更新色块列表过程，然后调用创建新组块过程；

如图10-5所示，是2号组块的触底、触块判断。我们应该想到，问题的答案就在色块列表中，通过对色块列表的遍历来求出所有填满的行(行号)，显然，我们应该在更新色块列表之后调用求填满的行。

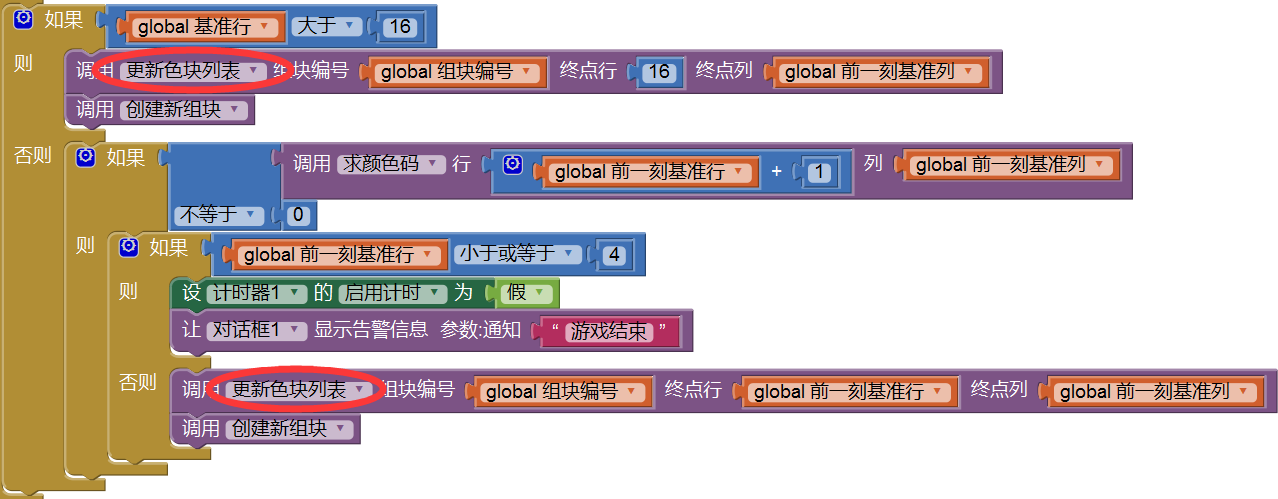
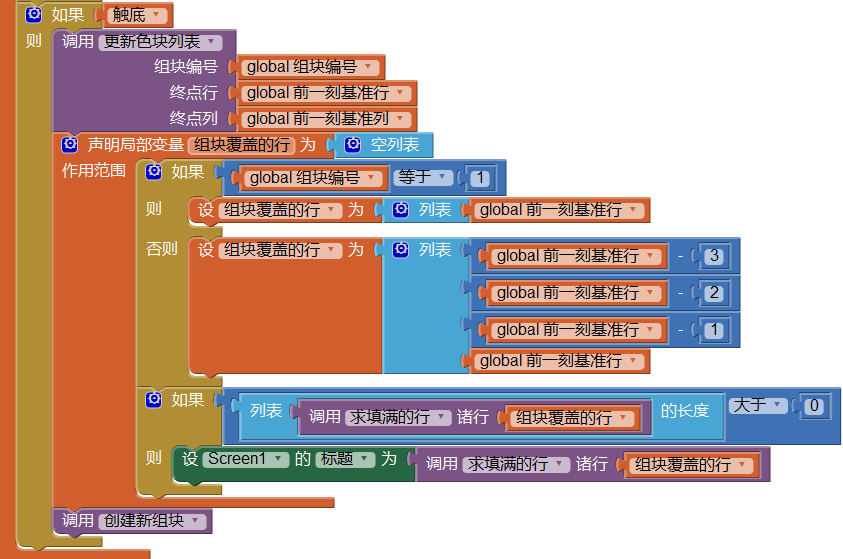
如图10-6所示，过程求填满的行的返回值是一个列表，其中的列表项为已经填满行的行号，我们在更新色块列表之后，判断该列表的长度是否＞0。如果列表长度＞0，意味着某一行或某几行被填满，需要从画布上消除这些行。

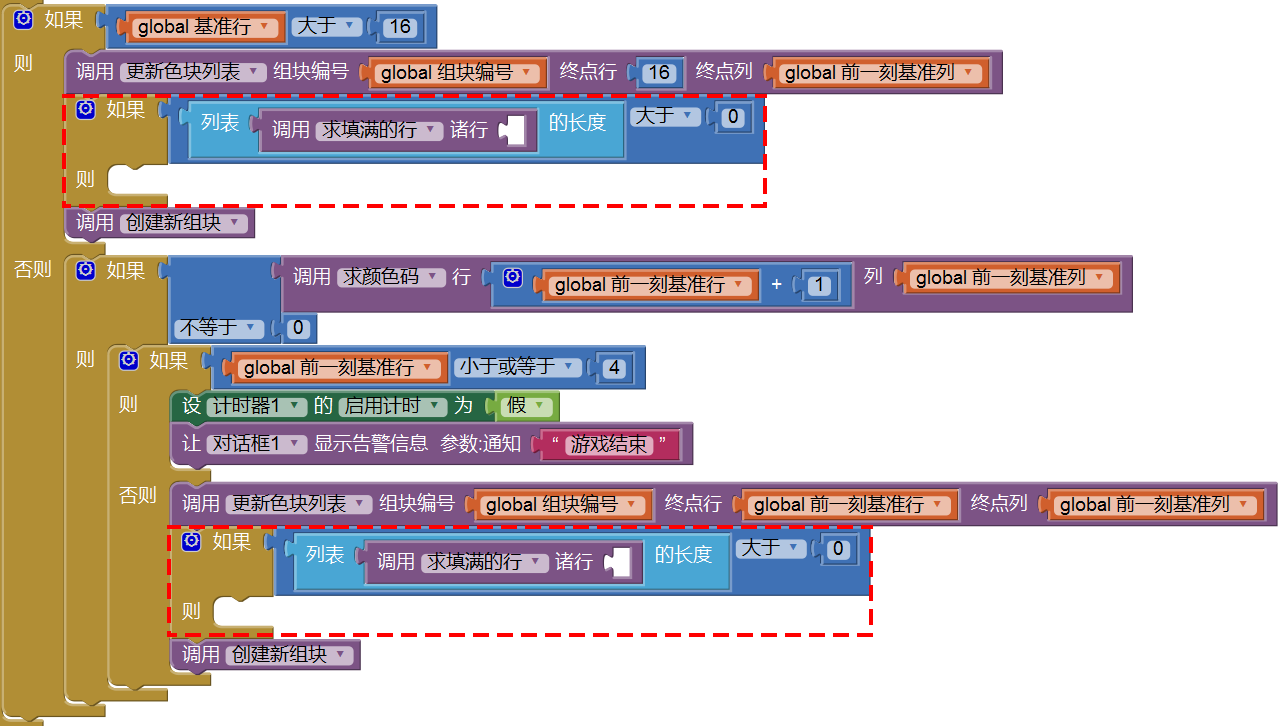
我们已经提到，在计时程序中，有四处停止下落的判断，这就意味着我们要在四个位置放置同一套代码，来判断是否有填满的行，并进行一些列的后续操作（消除填满的行、上面的行落下来等等），这不仅意味着这段代码的复用程度很高，同时也向我们提出要求，改进程序的结构，让这段代码在整个计时程序中只出现一次。

上一章中的图9-13是计时程序的最新版本，这个程序已经有太多行代码，逻辑也稍显复杂，而接下来对填满行的处理也将在这个程序中完成，因此，此时我们有必要对程序的结构作出调整，来适应更为复杂的逻辑。

第二节 改写计时程序

为了厘清程序的结构，我们来重温一下上一章第五节的流程图，如图10-7所示。

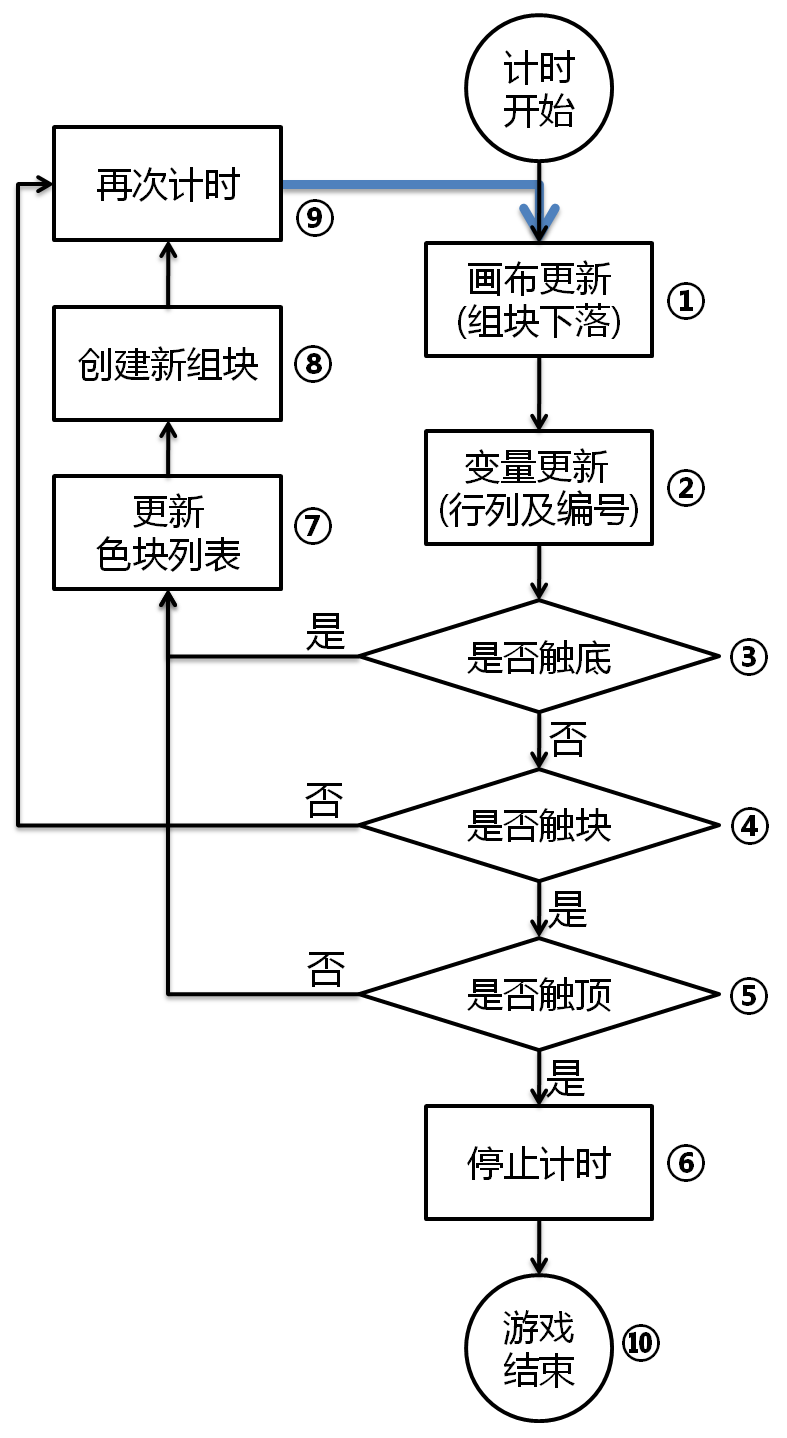
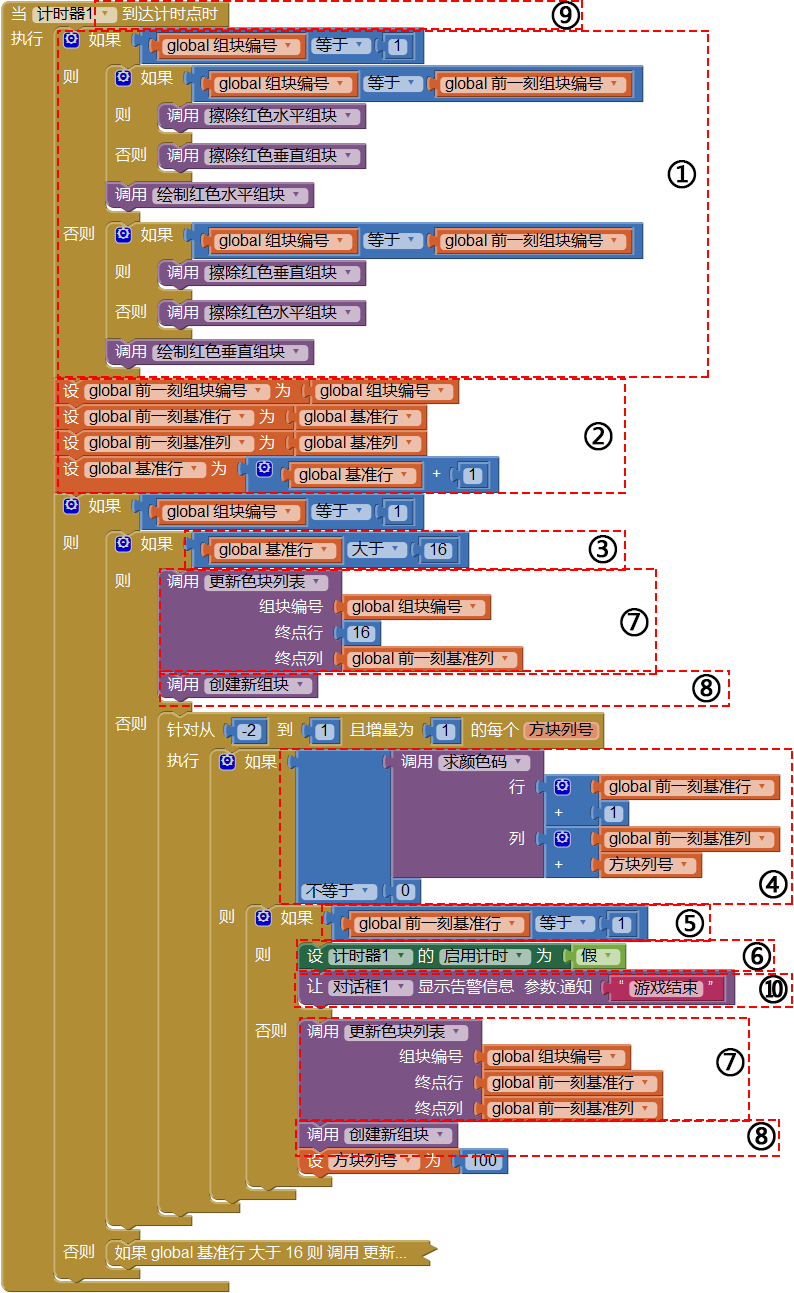
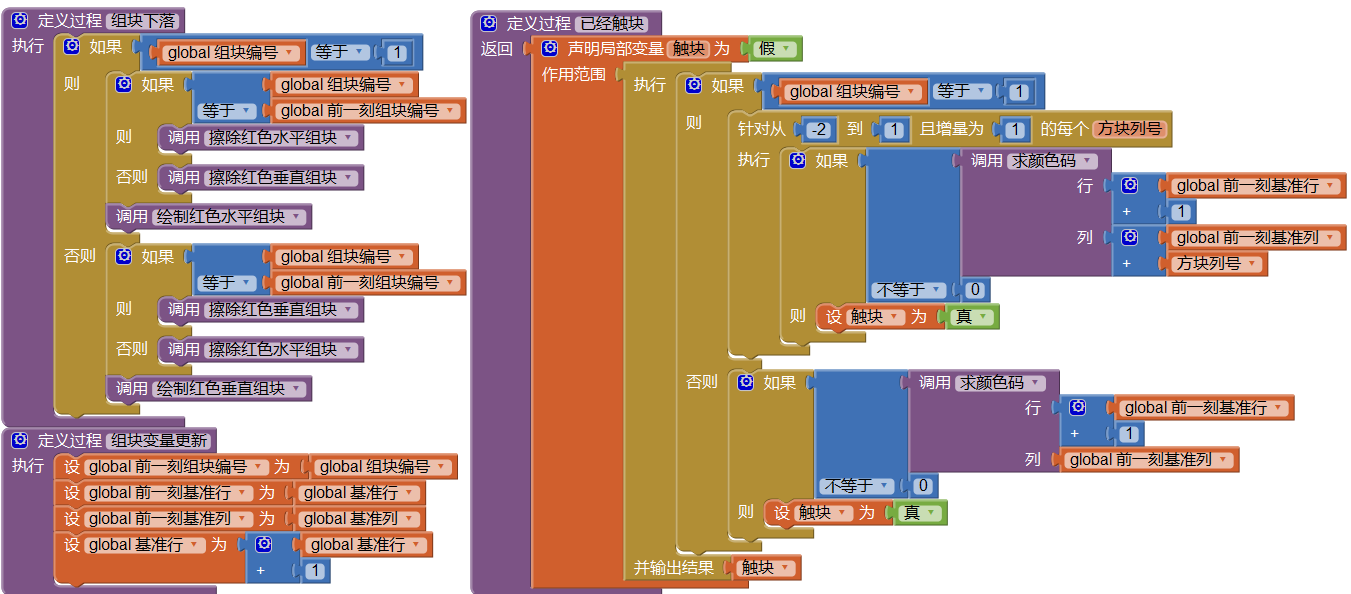
为了使程序尽可能的模块化，需要把一些固定不变的代码封装成过程，以便于调用和修改。我们将“画布更新(组块下落)”及“变量更新(基准行列)”这两部分的代码分别定义为两个过程组块下落及组块变量更新，另外，将触块判断定义为过程已经触块，如图10-8所示。已经触块过程具有返回值，如果已经触块，返回值为真，否则为假。

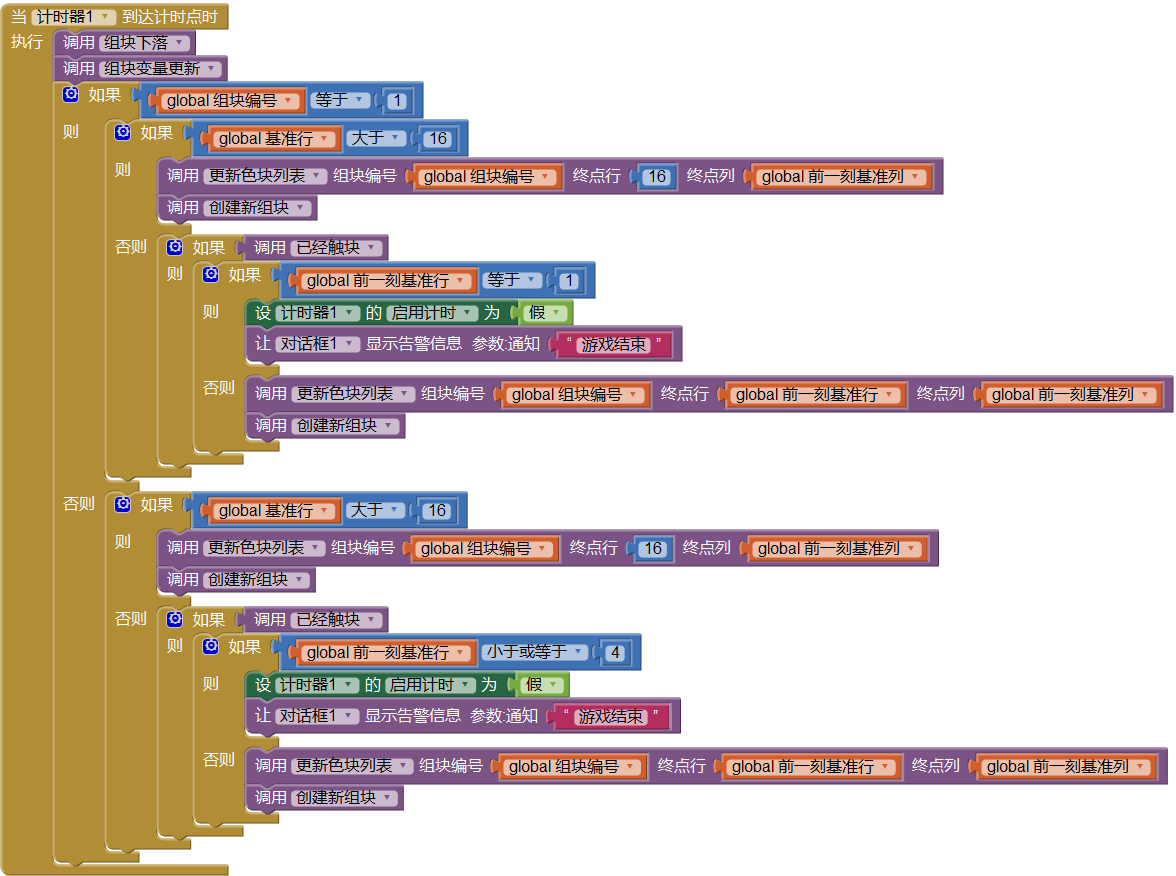
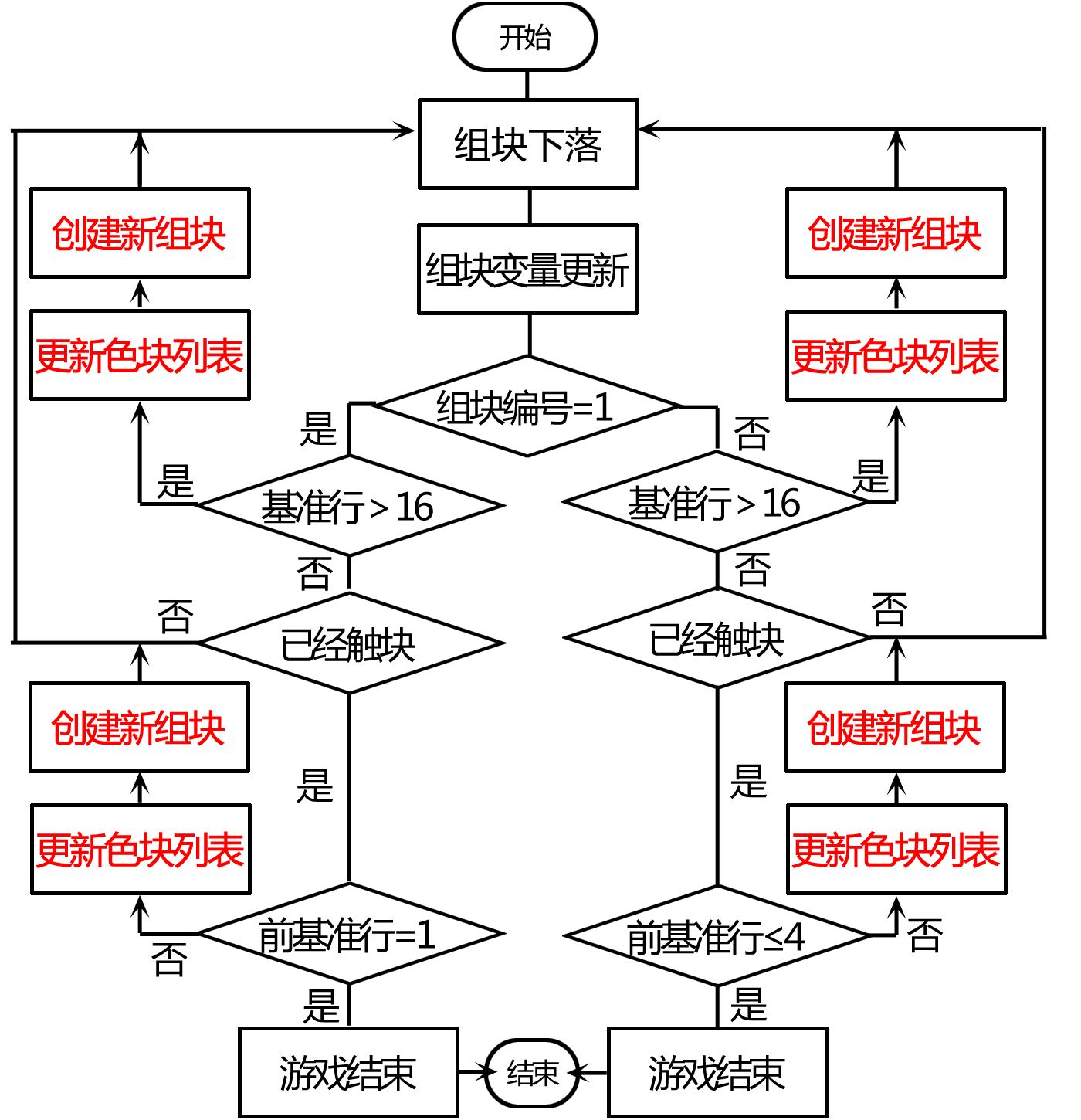
通过对比代码与流程图，我们发现更新色块列表及创建新组块被分别调用四次，已经触块被调用两次，“基准行＞16”语句被调用两次。程序中出现重复代码，为程序埋下了错误的隐患，如，当我们需要修改某些重复代码时，就有可能漏掉其中的一部分，这会造成程序的错误。这是程序结构的问题，需要加以调整，来消除这些重复的代码。我们希望调整的结果如图10-10所示。

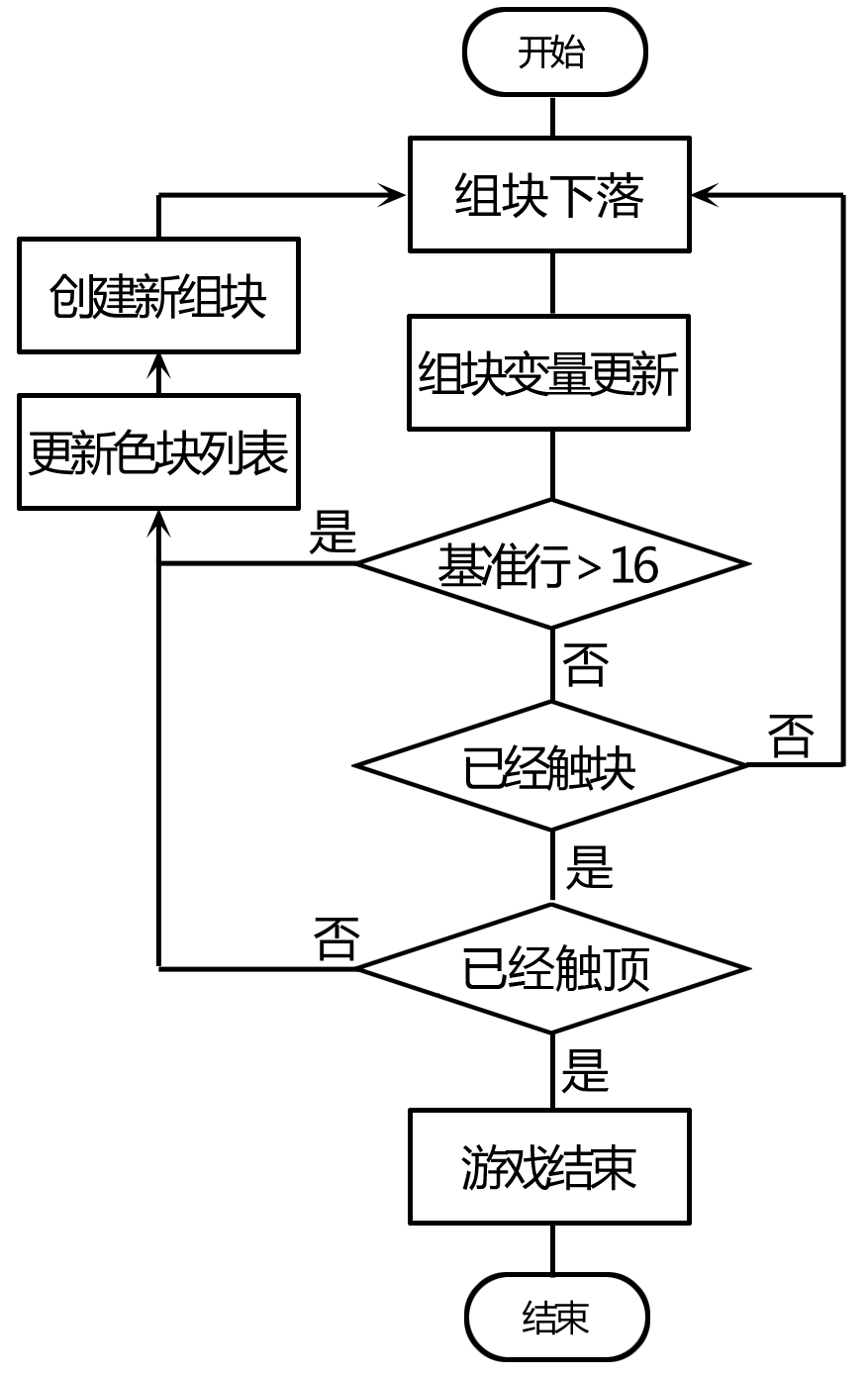
现在，我们可以把求填满的行过程添加到代码中，如图10-11所示，这里我们利用屏幕(Screen1)的标题属性来显示我们的运算结果：在右图中黄色区域是刚刚触底的2号组块，在屏幕的标题栏中，显示了它所填满的行：(13 14 15 16)，这是一个列表。

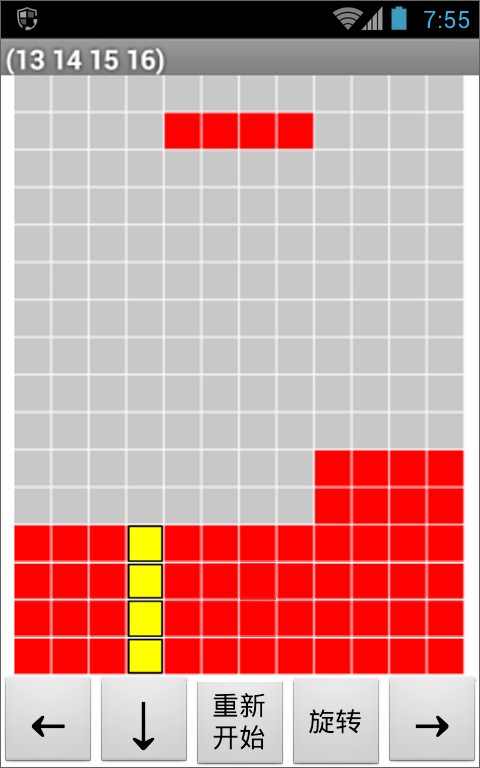
接下来要解决的问题是，当某些行被填满时，如何从画布上消除这些行。我们希望创建一个“消除行”的过程，来完成这样的操作，这正是下一节的内容。

第三节 消除被填满的行

消除被填满的行，这个行为包含了两项操作：①数据更新——将色块列表中填满行的列表项删除，并添加等量的值为0的列表项；②画面刷新——用修改后的色块列表重新绘制画布。本节讲述的是第一项操作，下节将讲述第二项操作。

定义一个没有返回值的过程消除行，来处理全局变量色块列表。在第一节我们定义了一个有返回值的过程求填满的行，利用该过程的返回值，我们可以有针对性地操作色块列表中的列表项。具体的操作是：删除被填满行的列表项，同时插入同等数量的值为0的新列表项，以保证色块列表的总长度为192。具体代码如图10-12所示。消除行过程的参数行号列表就是求填满的行过程的返回值。

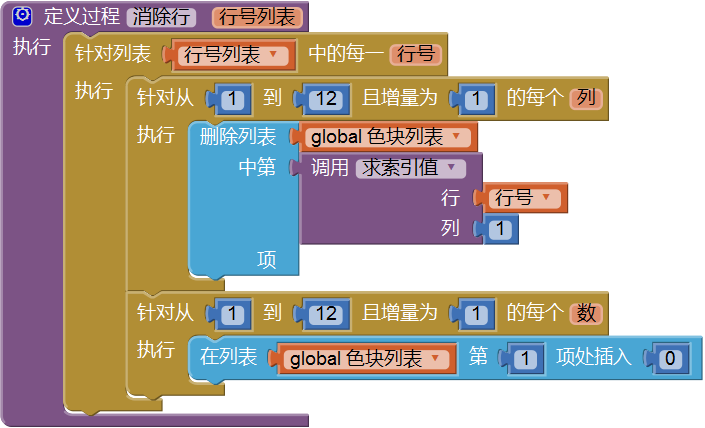
在这个过程里使用了双层循环：外层循环使用了遍历列表的循环语句，对已填满的诸行进行逐一操作；内层有两个循环语句，第一个用来删除指定行、列值的列表项，第二个用来在列表的首位插入一个值为0的列表项。

如果你仔细观察，可能会对两处代码产生疑问：①为什么在删除列表项的操作中，求索引值过程的列参数值总是1？②为什么要在整个列表的首位插入新的列表项，而不是在刚刚删除的位置插入列表项？这两个问题与列表的特性有关，我暂时不作回答，留待本章的第五节再做解释。

接下来的问题是：在哪里调用消除行过程？我们说过，组块的任何行为都发生在计时程序中，因此消除行也不例外。如图12-13所示，当求填满的行返回的列表长度＞0时，执行消除行。这里我们保留了在屏幕的标题栏显示填满行列表的语句。

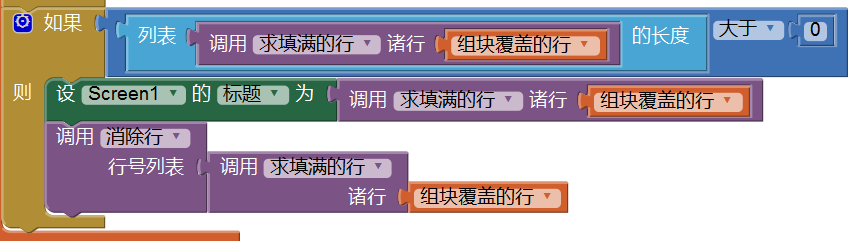
如果现在我们连接手机进行测试，当组块填满某些行时，标题栏会显示这些行的行号，但填满行的彩色方块并没有从屏幕上消失，而后续落下的组块会从那些理应被消除的块上扫过，所过之处，彩色方块变成灰色方块，这说明色块列表已经被更新。这当然不是我们想要的结果，不过离目标——从画布上消除那些已填满的行仅一步之遥。这正是下一节要讲述的内容。

第四节 让填满的行从画布上消失

从画布上消除这些填满的行，并让上面的行落下来，这是本游戏中的最后一项难题，看我们如何来解决它。

上一节我们完成的对色块列表的更新，删除了已填满行的列表项，并插入同等数量的值为0的新列表项，这样处理之后的色块列表依旧具有192个列表项，这一节，我们将依据这个新的色块列表，在画布上重新绘制色块。如图10-14所示，我们定义了一个无返回值过程“重绘画布”，并在计时程序中消除行的后面调用它。

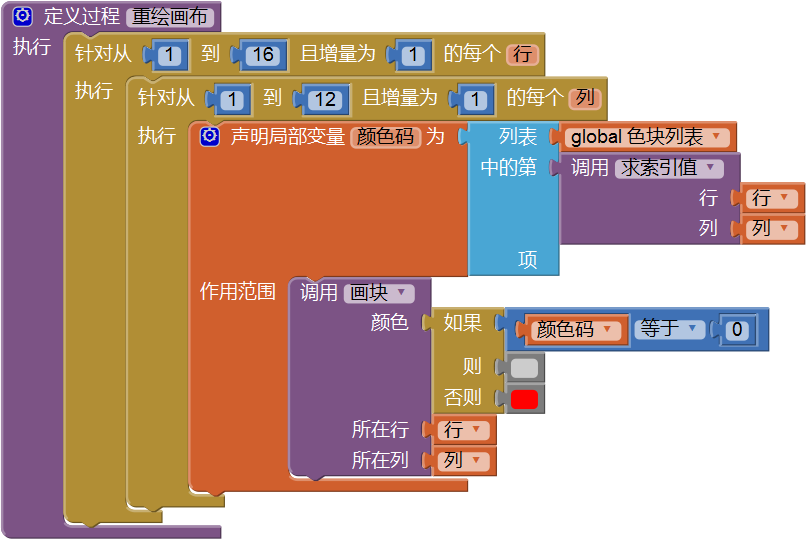
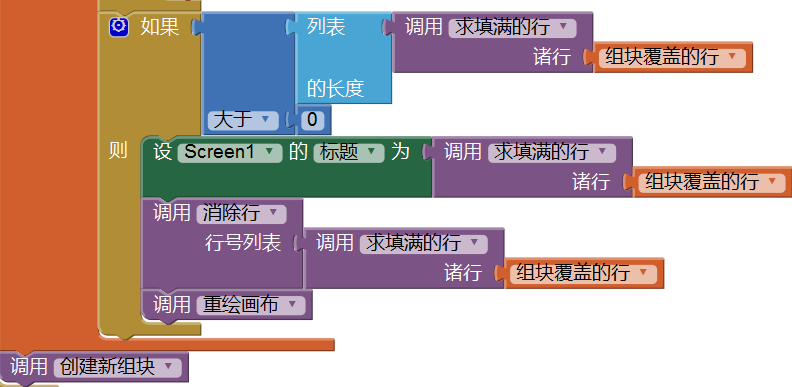
留心图10-14中画块过程的颜色参数，此处使用的是条状组块特有的红色，我们会在后面的章节中改造这一参数。

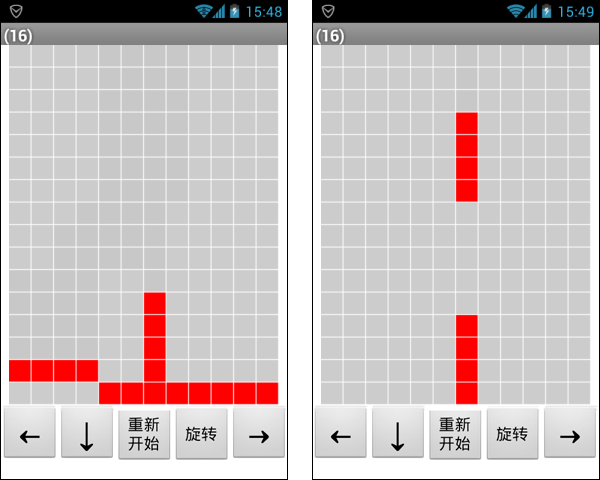
现在我们可以对程序进行实时测试了。我们利用三个1号组块填满第16行，如图10-15所示，但情况并非如我们想象的那样。当最后下落的1号组块（左侧）下落到第15行时，画面出现了一段时间的停滞，此时屏幕标题栏显示了“(16)”，如图10-15左侧的手机截屏所示，这意味着求填满的行过程已经运行完毕。随后最后一行的两个1号组块和第15行的1号组块消失，原来处在第15行的2号组块落到第16行，同时新生成的组块开始下落，如图10-15右侧的手机截屏所示。

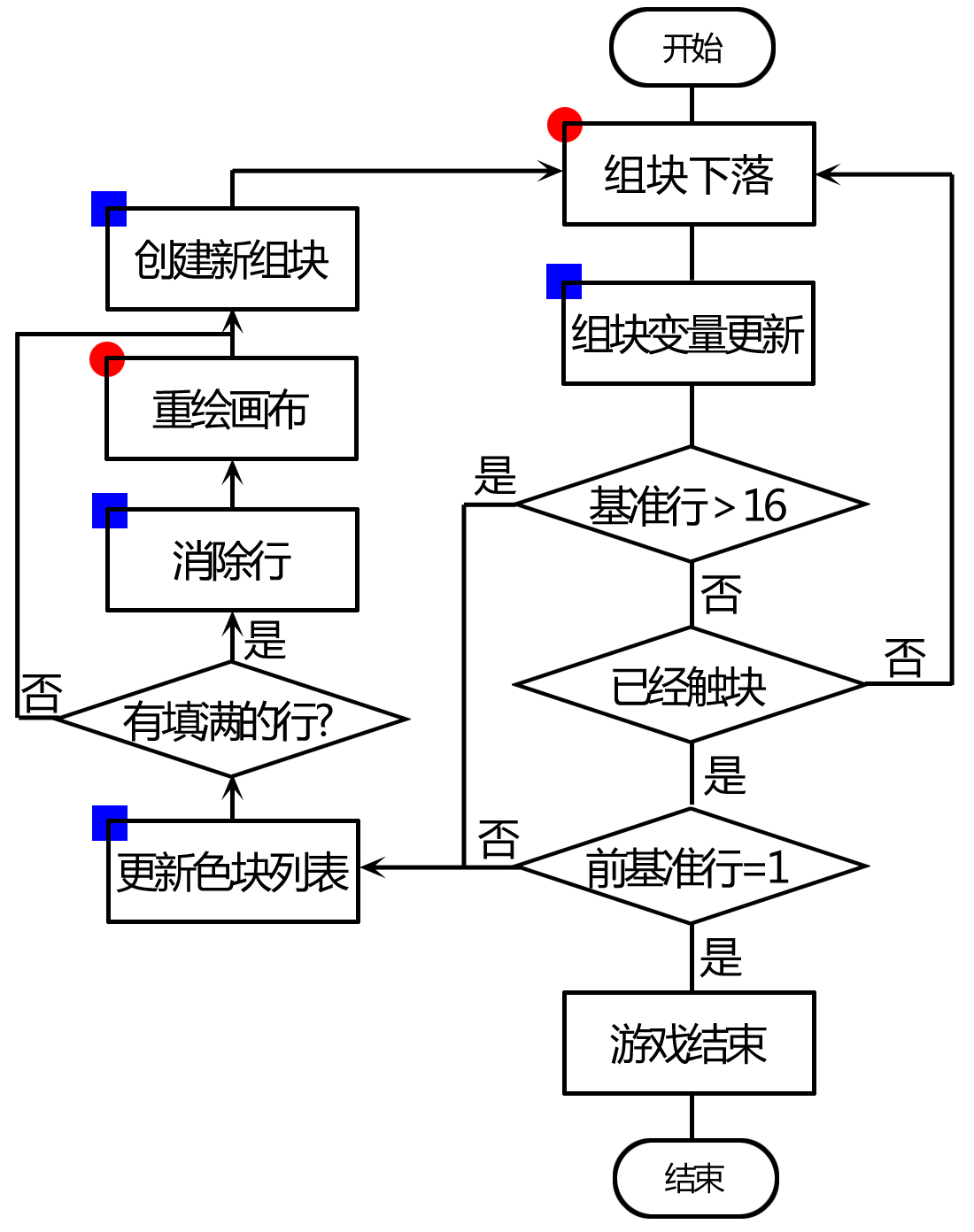
我们来分析一下出现这种现象的原因。如图10-16所示，这是截至目前为止计时事件处理程序的流程图，在图中我们用蓝色方块表示对数据的更新处理，用红色圆形表示对画布的刷新。在添加重绘画布过程之前，组块的下落没有异常，在调用了重绘画布之后，组块停留在第15行，而数据已经判断出第16行被填满（屏幕标题栏显示(16)），这说明此时更新色块列表的操作已经完成。为什么在第16行绘制1号组块的组块下落过程没有被执行呢？它在计时程序中的位置分明是在更新色块列表之前，应该先于更新色块列表执行。

这个问题的产生，最终要归结于安卓设备的CPU(中央处理器)要处理两种不同类型的操作：计算与输入输出。计算发生在CPU内部，就像我们的大脑，思考和判断仅在一念之间；而输入输出发生在CPU与外部设备之间，本段程序中涉及到输出操作，CPU要将计算结果输出到外部设备——显示屏上，就像我们要用纸笔把想到的事情写出来一样。两种类型操作的运行效率差别很大，以至于等不到组块下落步骤的完成，程序就已经开始执行重绘画布的操作，并继而进入到下一次计时事件之中了。

这个问题可能还有另一种解释，也与两种不同类型的操作有关：当同时有计算和输入输出任务需要CPU处理，而CPU在同一时间只能处理一项任务时，通常计算任务具有更高的优先权，输入输出任务要让位于计算任务，这就是所谓的CPU的单线程。

解决这个问题的思路有两条线索：①改进画面更新的程序，减少重绘画布的循环次数；②调整两种类型操作的执行顺序，先计算，后刷新屏幕。

先来尝试减少重绘画布的循环次数。在图10-14的左图中，我们用了双重循环来重绘画布，外层循环遍历所有的行，这其中可能存在一些不需要重绘的行，比如那些没有彩色方块的，位于画布顶端的行。我们最好能够准确地知道哪些行需要重绘，哪些行不必重绘。这里我们声明两个变量，重绘起始行和重绘终止行，简称起始行、终止行，看看能否通过减少重绘的行数，来改进屏幕刷新的速度。

假设起始行与终止行的初始值为16，即最底下的行，现在来明确它们的意义。起始行：从画布顶端开始向下检查，首次出现彩色方块的行，定义为起始行；终止行：组块下落所覆盖的行中，最下面的一行，定义为终止行。那么介于起始行与终止行之间的行，就是需要重绘的行。

如何获得这两个变量的值，是接下来要考虑的问题。起始行：从游戏计时开始，第一个组块触底，组块最上面的行就是起始行，后来触底的组块与之前的起始行进行比较，并将较小的值设为起始行。终止行：当组块触底后，可能被填满的最大的行，就是组块最下面的一行，按照我们最初的约定，组块最下面的行就是“基准行”或“前一刻基准行”，这要看我们取值的位置。下面用代码来实现我们的设想，如图10-17所示。

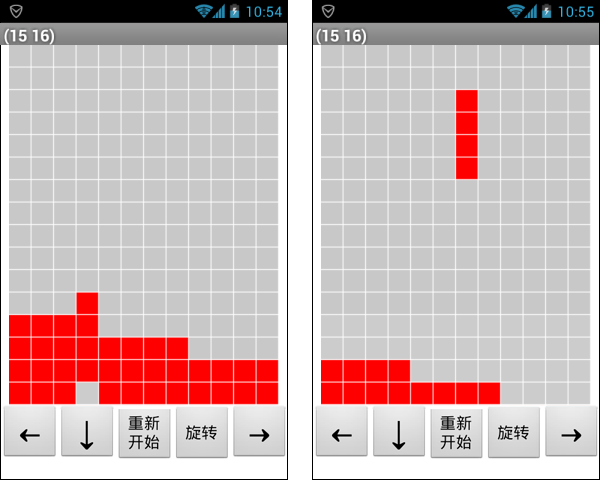
从直观的感觉上讲，画面的刷新速度有些许的改进，但并没有在组块触底并填满行的一刹那，实现关键组块在屏幕上的组块下落操作，最后落下的填满行的组块依然是不能下落到应有的位置，但程序已经开始重绘画布，紧接着新的组块出现在屏幕顶端，并开始下落，如图10-18所示。

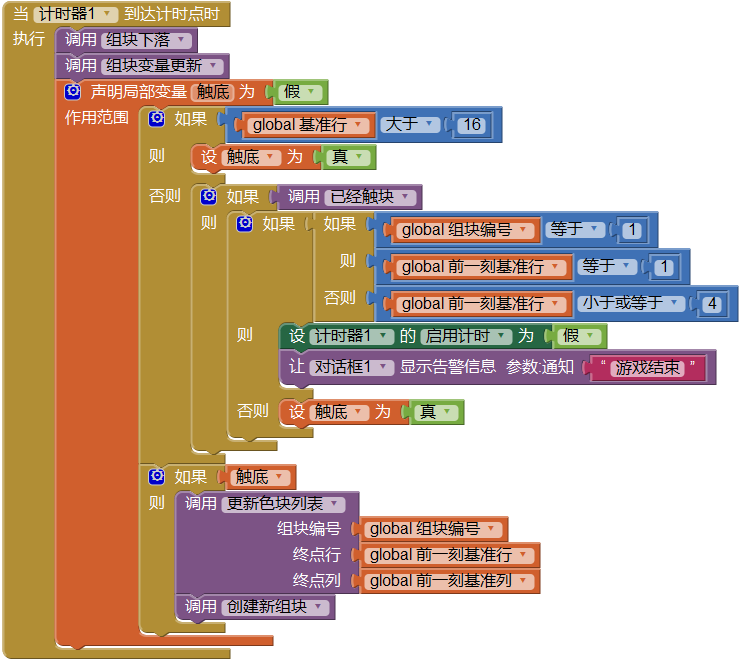
为此，我们不得不再去尝试第二种改进方案——调整程序的执行顺序：先进行判断，并依据判断结果执行不同操作，改进后的程序流程图如图10-19所示。图中红色方框表示对画布的更新处理，其余方框是对数据的处理，粉红色线条表示游戏结束流程。经过这样的调整，最终解决了填满行组块不能下落到位的问题，如图10-20所示。

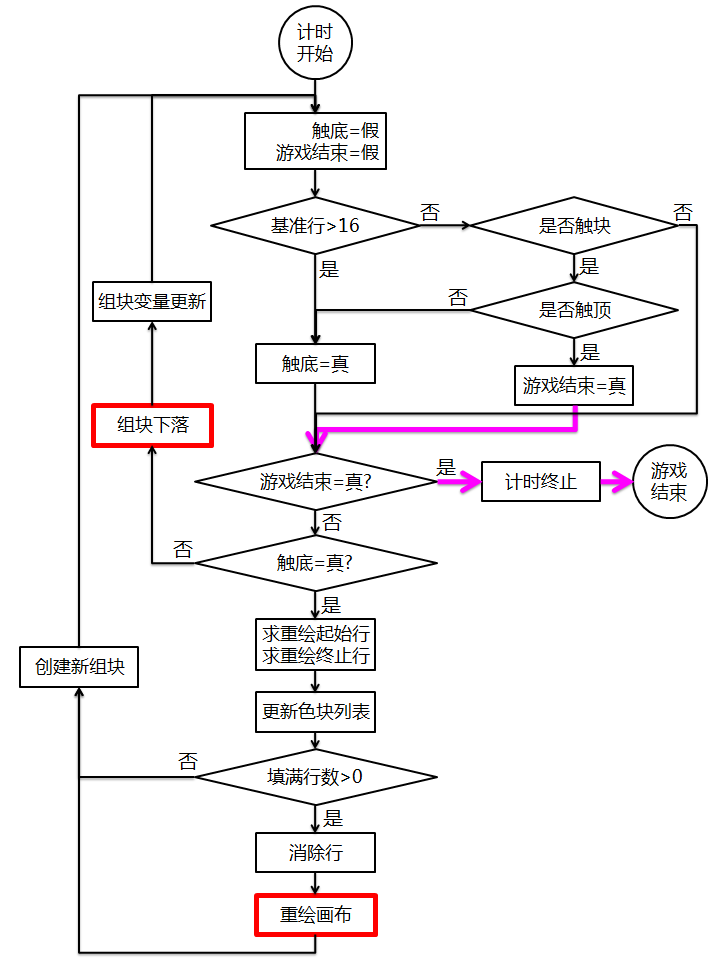
改进后的程序将逻辑判断与具体操作分离开来。首先添加两个局部变量触底(包括触块)、游戏结束，并设其初始值均为假，即假设程序开始运行时，组块既没有触底（或触块），也没有触顶（游戏结束）。我们来分析组块触底前后的三个计时周期内程序的运行过程，看看这样的调整是如何起作用的。

• 我们研究的第一个计时周期，假设2号组块已经在屏幕上落到了第15行（已经执行完组块下落操作），之后对组块变量进行更新（执行组块变量更新过程），让基准行=16，前一刻基准行=15，程序进入下一个计时周期；
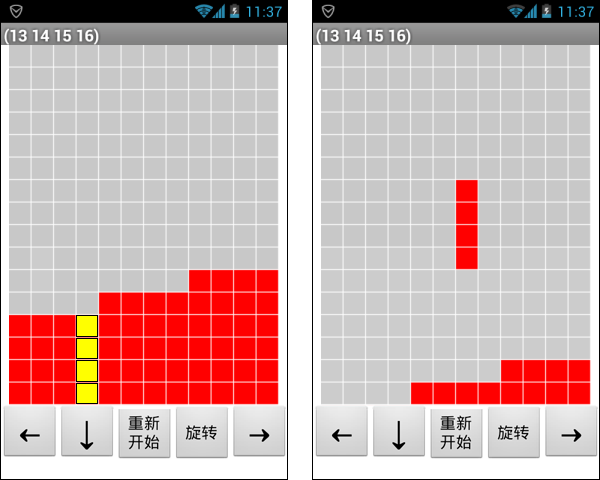
• 在我们研究的第二个计时周期开始时，基准行=16，前一刻基准行=15，因此，触底=假，游戏结束=假，程序将执行组块下落过程，即在第16行绘制2号组块，这正是图10-19右图中黄色方块所在的位置，然后程序执行组块变量更新过程，即，让基准行=17，前一刻基准行=16，程序再次进入下一个计时周期；
• 在我们研究的第三个计时周期开始时，基准行=17，因此，触底=真，游戏结束=假，程序将执行更新色块列表过程，并进行填满行的检测，由于已经触底的2号组块刚好填满了13~16行，因此填满行列表的长度＞0，程序将执行消除行及重绘画布过程，然后创建新组块，并进入下一个计时周期。

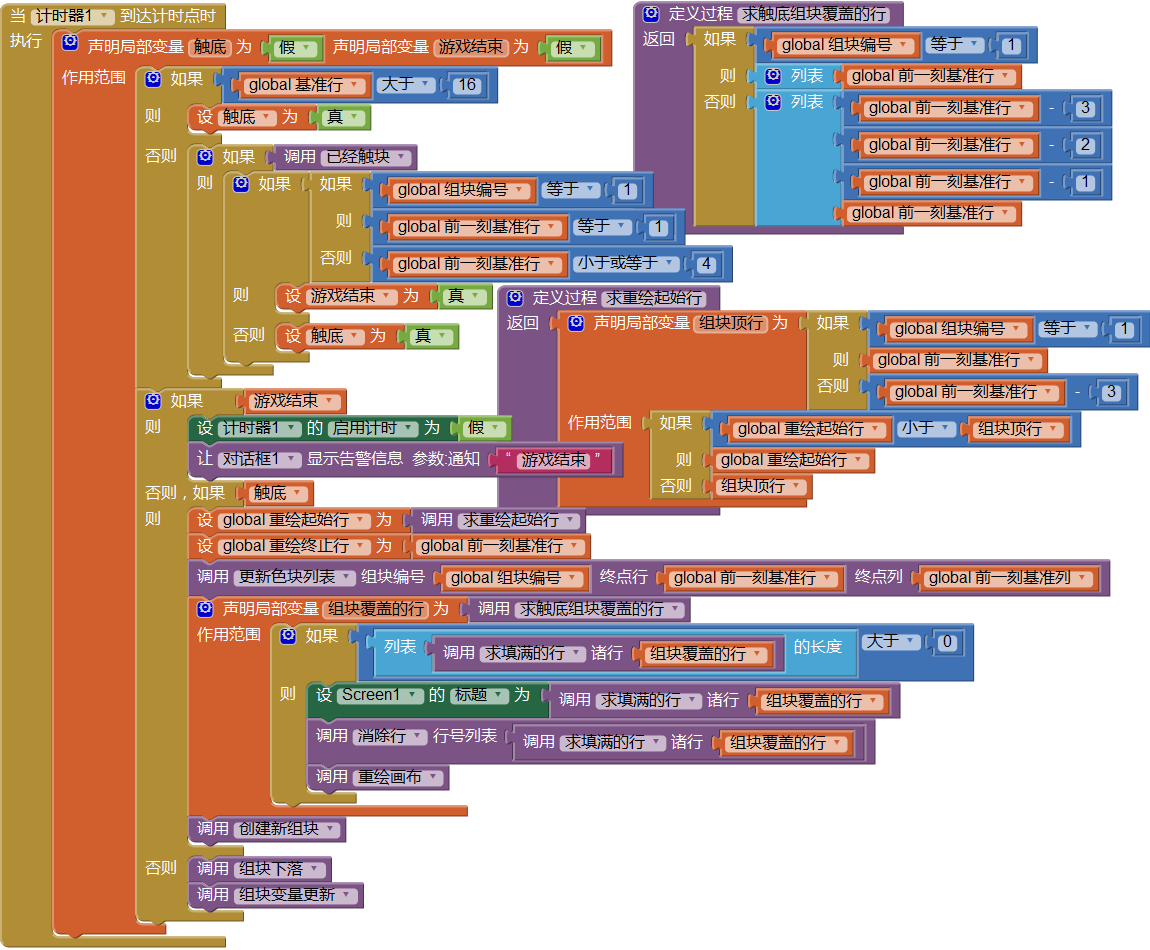
通过对以上三个计时周期的分析，我们可以总结出程序的两个特点：

1. 在每个计时周期中，首先对下落组块的状态进行判断（是否触底、触顶），并依据判断结果，执行不同的屏幕刷新操作（组块下落或重绘画布）；
2. 组块下落与重绘画布这两个屏幕刷新操作分别处在两个不同的计时周期中。

我在制作第一个版本的俄罗斯方块时，其实并没遇到这个问题，可能是某种习惯，让我很自然地写出了正确的代码。但在编写这本开发笔记时，我没有按照原来的版本组织代码，结果遇到了这个问题。为了解决这个问题，我做了各种尝试，甚至包括将计时周期划分为奇数周期和偶数周期，试图将画面的刷新与数据的更新分别放在不同的计时周期中处理，这使得程序变得更为复杂。虽然最终还是放弃了这种方案，但这种解决问题的思路还是体现在图10-21的代码中。

第五节 列表项的删除与插入操作

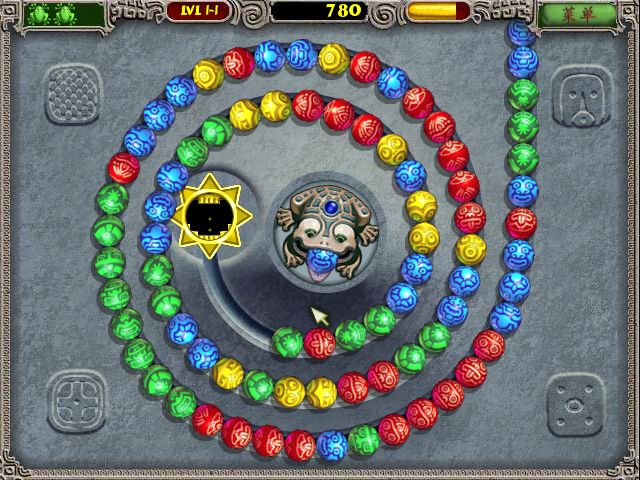
如果你玩过一个叫“祖玛”的游戏，你一定知道那只盘踞在圆心的青蛙，它吐出的彩球会插入到正在行进的彩球队列中，当新加入的彩球与相邻的彩球颜色相同，且同色球的数量≥3个时，这组彩球将集体毁灭，此时，如果断点前后的球同色，则这些球会迅速靠拢，当合并后的同色球数量≥3时，这些同色球也将集体毁灭，然后，断点前后的球将继续靠拢......无论这些球是向前或向后靠拢，它们之间的顺序不会该变。这个场面非常适合来解释列表元素的插入与删除操作。

一、列表项的删除

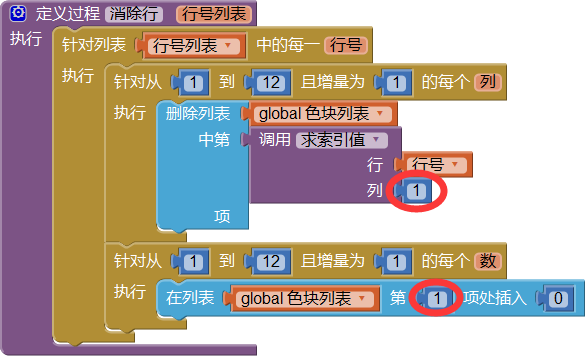
在本章的第三节中，我们定义了消除行过程，来删除色块列表中已经填满行的列表项，并同时插入的等量的值为0的新列表项，如图10-23所示。当时我们遗留了量个问题，①为什么在删除操作的循环中，求索引值过程的参数列的值始终是1，而与循环变量列无关；②为什么始终都在列表的首位插入新的列表项。这里我们将给出解释。

列表变量是一系列元素的集合，它们按照设定的顺序排列，这种顺序是有意义的，这个意义体现为列表项的索引值。假设有一个字母列表(A,B,C,D,E,F,G)，给它起名叫list，它共有7个元素，其中A的索引值为1，G的索引值为7，列表的长度为7。

为了方便说明，我们新建一个项目，在用户界面上添加一个按钮、一个标签，如图10-24所示。点击按钮将为实验列表添加7个列表项，然后在循环语句逐个删除列表项，并显示剩余列表项。

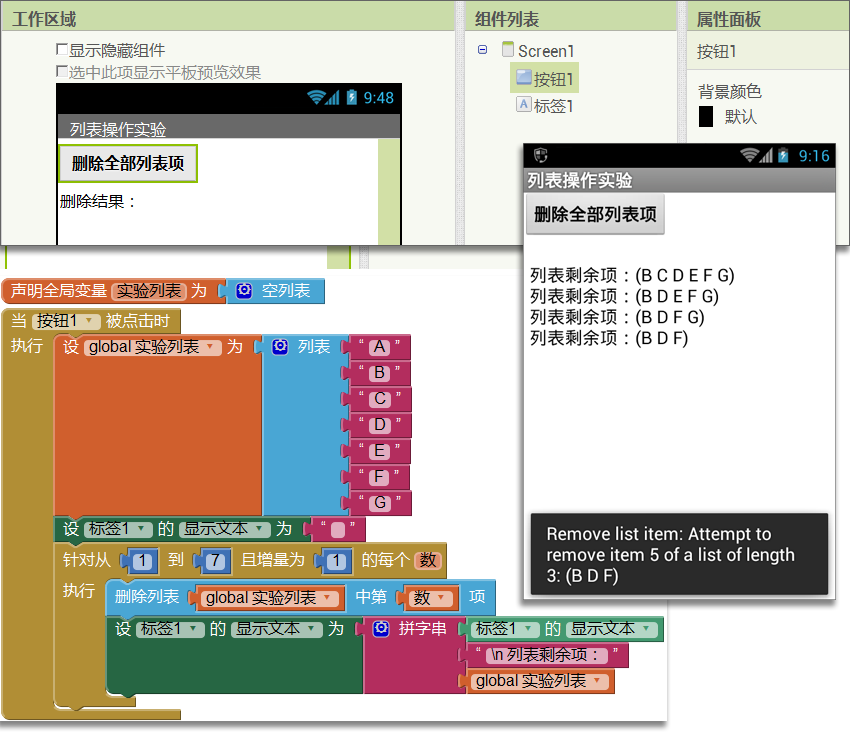
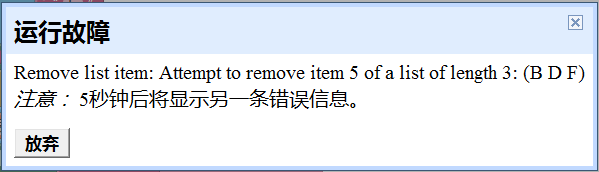
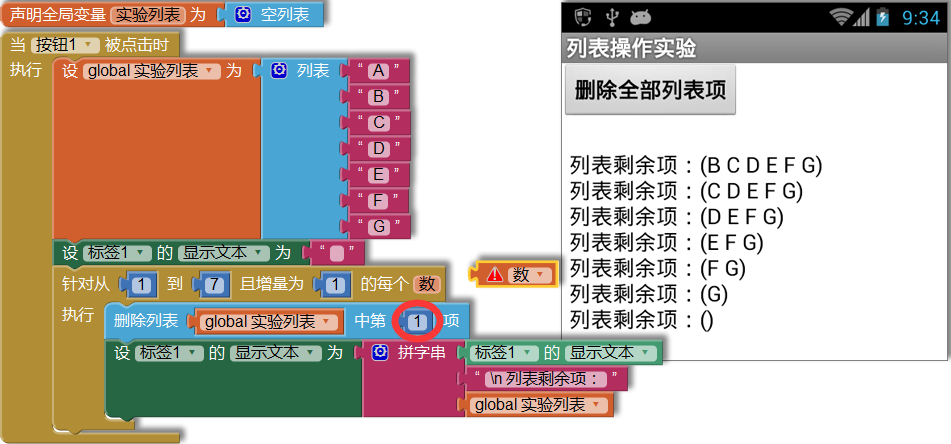
注意观察程序在手机上进行测试的结果： ● 首次循环，索引值=1，执行删除操作之后，列表剩余项为(B C D E F G)，A被删除； ● 第二次循环，索引值=2，执行删除操作，想想看，被删除的应该是什么？是“C”，这时列表剩余项为(B D E F G)，因为此时C的索引值为2； ● 第三次循环，索引值=3，将删除E，此时列表剩余项为(B D F G)； ● 第四次循环，索引值=4，将删除G，列表剩余项为(B D F)。 此时，手机和电脑的编程视图中分别出现错误信息。译为中文是说，试图从长度为3的列表中删除第5项，这说明错误出现在第五次循环，如图10-25所示。

下面我们把删除操作中的“索引值”换成数字“1”，再看运行结果。如图10-26所示，每次循环都从列表中删除第1项，七次循环结束时，列表为空。

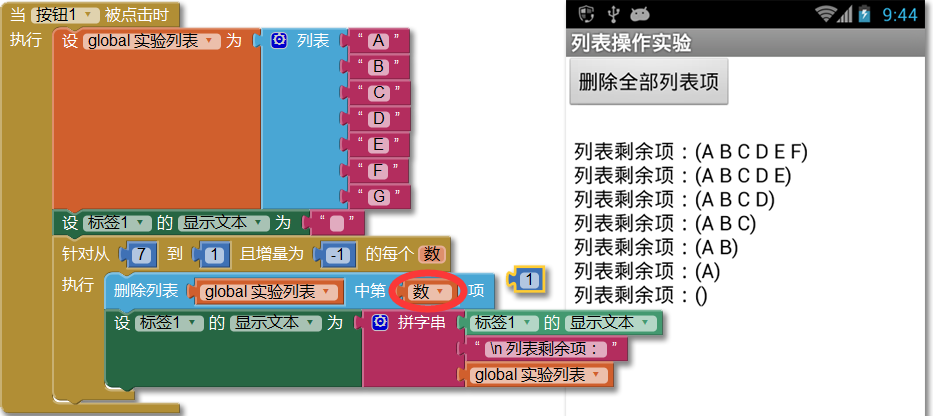
除此之外，还有一种方法也可以安全地删除列表中的每一项，即，设循环变量的起始值为7，终止值为1，增量为-1，并在删除操作中引用循环变量，也可以得到图10-25的结果。如图10-27所示。这是因为从列表的末尾删除一项，并不会改变其余项的索引值。

在游戏开发中，经常会涉及到对列表的操作，删除所有列表项的操作也时有发生，因此要小心地对待循环变量的引用，避免发生上述错误。

二、列表项的插入操作

App Inventor中的列表变量，其中的元素——列表项，就像祖玛游戏中的彩球队列一样，可以在列表的任何位置插入新的列表项。插入新列表项之后，新项之前的列表项索引值不变，新项之后的列表项索引值+1。如果将新项插入到列表的首位，即索引值为1的位置，则原来所有列表项的索引值+1。

在本章创建的消除行过程中，先后对列表项执行删除及插入操作。如图10-28所示，在消除行的外层循环中，首先删除了填满行的12个列表项，然后又向列表首位插入了12个值为0的新列表项。对色块列表的删除操作，从数据上实现了删除填满的行，而在列表首位插入等量的新列表项，让原有列表项的索引值等量增加，以保证色块列表的列表项总数不变（192个），为下一步的重绘画布提供了正确的数据。我们来看看消除行的定义与调用，以及与之相关的过程，。

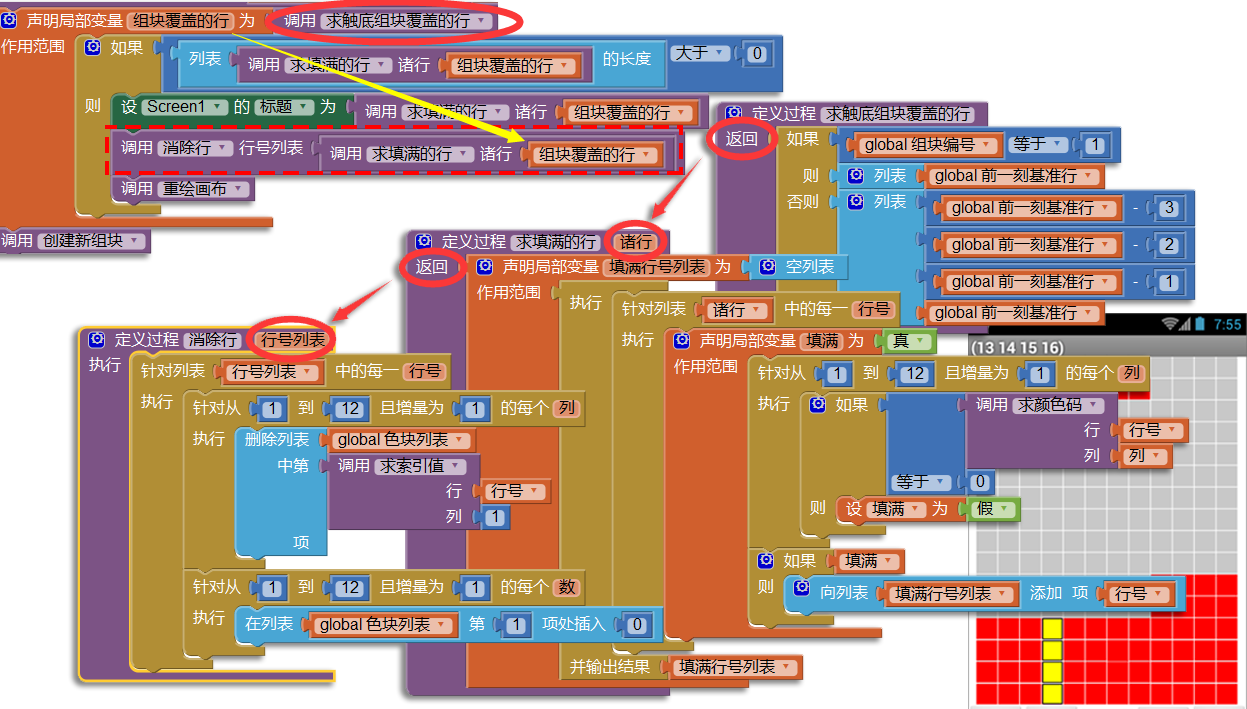
现在假设触底组块为2号组块，如图右下角所示，这时求触底组块覆盖的行过程的返回值为列表(13,14,15,16)，注意列表元素的顺序是从小到大，这正是过程求填满的行的输入值，即参数诸行的值；而求填满的行的返回值也是列表(13,14,15,16)，该值是过程消除行的输入值，即参数行号列表的值。下面来分析消除行的执行过程。

在消除行中，第一次外层循环行号=13，程序删除了第13行中的12个列表项，之后又在列表首位插入了12个值为0的新列表项，这相当于在列表中添加了一个新行，新行对应于画布最上面一行。对于第14、15、16行而言，在删除第13行之后，他们的索引值将分别减小12，也就是行数分别减小1，如，第16行将变为第15行，此时如果没有插入一个新行，那么在第二次循环中，被删除的将不是第14行，而是第15行。由于在删除之后添加了等量的列表项，因此保持了14、15、16行列表元素的索引值不变（也就是它们在列表中的位置不变），因此也就保证了后续的外层循环能够正确地删除那些填满行的列表项。

列表项的插入与删除操作，是两个被广泛而频繁使用的操作，尤其是在游戏软件开发中，经常被用来操作画面上的显示对象，因此，正确地理解这些操作规则，对游戏开发者来说，是非常重要的。